给定一个点集,有无数个圆可以对其进行覆盖,如何找到半径最小的那个圆?如果暴力求解,将会是四次方的时间复杂度。本文将介绍主流的通过随机增量实现的在期望上具有线性的时间复杂度的最小圆覆盖算法,阐述算法流程,并给出直观易懂的证明,还展示了递归和递推两种代码实现。
本文封面由MATLAB绘制,代码由gemini编写。
算法流程
流程说明
基于随机增量的最小圆覆盖算法精髓在于“增量”。本节将重点说明算法里是如何运用增量的。在这一节里,不会对算法的严谨性进行过多的讨论,只会从一个直观上的感觉让人感觉是自然而正确的。
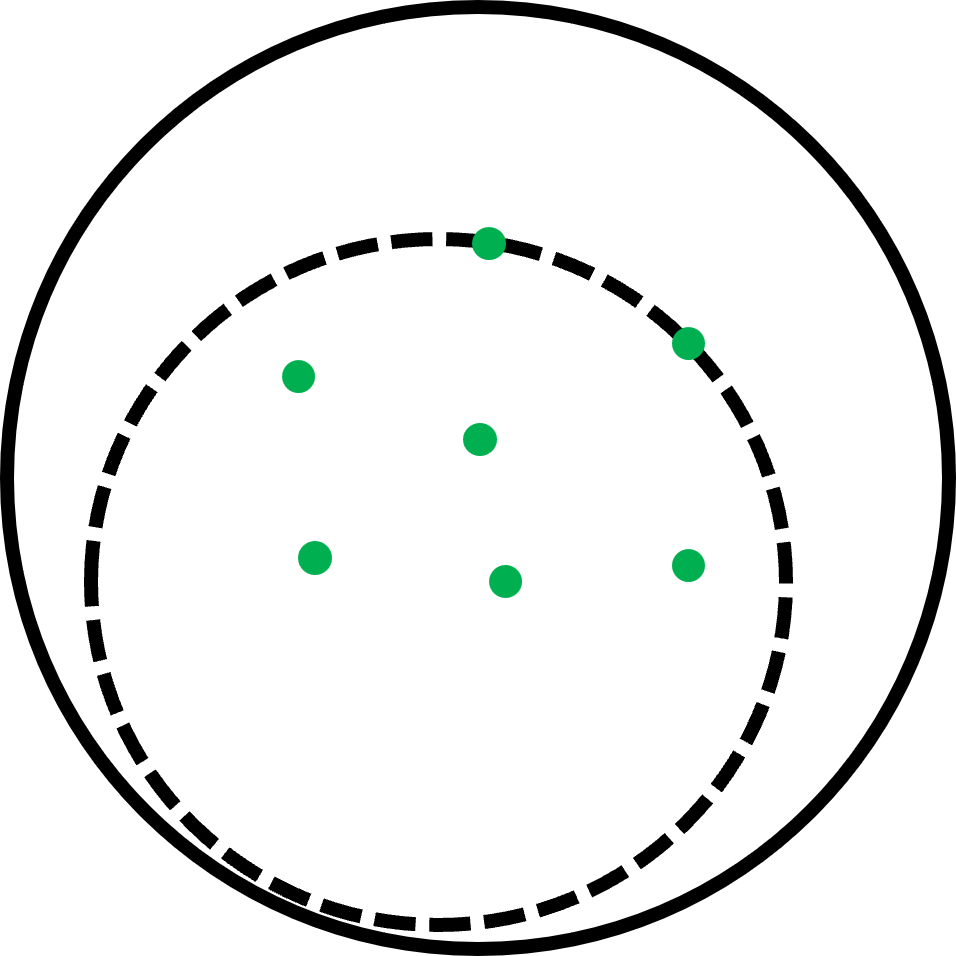
首先,由初中的平面几何知识,我们知道一个圆最多由三个边界上的点就能确定。从直观上来说,一个点集的最小覆盖圆边界上一定有点集里的点,否则覆盖圆可以进行收缩而变得更小。对于一个多于1个点的点集,最小覆盖圆的边界上一定有至少两个点。
比如左图中实线覆盖圆边界上没有点,就可以把覆盖原进一步缩小为虚线覆盖圆,那么实线覆盖圆就一定不是最小覆盖圆了。
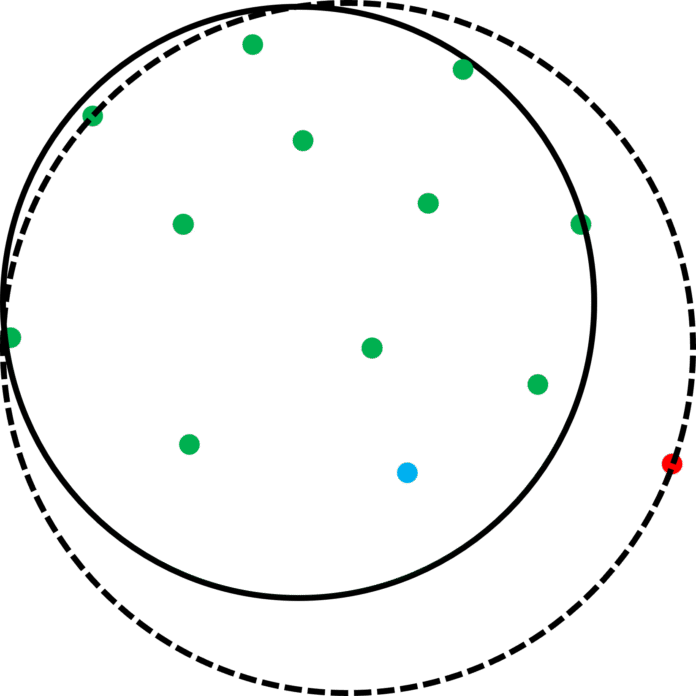
如果点集只有一个点,那么最小覆盖圆就是以该点为圆心、半径为0的圆;如果点集只有两个点,那么最小覆盖圆就是以该两点线段作直径的圆。我们使用$\mathrm{MEC}(\{P_1, P_2, \dots, P_k\})$ 表示由点集 $\{P_1, P_2, \dots, P_k\}$ 构成的最小覆盖圆(Minimum Enclosing Circle)。假设我们已经有 $\mathrm{MEC}(\{P_1,\dots,P_{i-1}\})$,现在需要求$\mathrm{MEC}(\{P_1,\dots,P_{i}\})$。看看 $P_i$ 在不在$\mathrm{MEC}(\{P_1,\dots,P_{i-1}\})$里面;在的话就还是这个圆;不在的话,我们可以断定$P_i$ 会出现在 $\mathrm{MEC}(\{P_1,\dots,P_i\})$ 的边界上。
比如左图,绿色的点表示已经找到最小覆盖圆的点集,蓝色和红色表示新加入的点的两种情况,现在需要找新点集的最小覆盖圆。如果新加入的点是蓝色点,它已经在之前的最小覆盖圆内,那么新点集的最小覆盖圆还是之前的圆;如果新加入的点是红色点,它在之前的最小覆盖圆外,那么新点集的最小覆盖圆需要更新,我们可以断定红色点一定在新点集的最小覆盖圆边界上。
好了,现在你已经开始学习这个算法最关键的部分了。我们现在的问题是需要重新求$\mathrm{MEC}(\{P_1,\dots,P_{i}\})$,知道的信息是$P_i$在这个最小覆盖圆的边界上。接下来,我们需要对点集$\{P_i, P_1, \dots, P_{i-1}\}$求经过$P_i$的最小覆盖圆。
最开始是确定$\{P_i\}$的单点最小覆盖圆,然后扩充到$\{P_i, P_1\}$的两点覆盖圆(在这一段接下来所说的最小覆盖圆都默认是经过$P_i$的点集的最小覆盖圆),慢慢地拓展到$\{P_i, P_1, \dots, P_{i-1}\}$的这个点集的最小覆盖圆。假设已经确定了 $\{P_i, P_1, \dots, P_{j-1}\}$的最小覆盖圆,现在需要加入$P_j$($j < i$)。和之前拓展点集一样,如果新加入的点在当前最小覆盖圆内,新点集的最小覆盖圆保持不变;如果新加入的点在当前最小覆盖圆外,那么要更新最小覆盖圆,和之前一样,我们能得到的信息是$P_j$在经过$P_i$的点集$\{P_i, P_1, \dots, P_{j}\}$的最小覆盖圆的边界上。接下来,我们需要对点集$\{P_i, P_j, P_1, \dots, P_{j-1}\}$求经过点$P_{i}$和$P_{j}$的最小覆盖圆。
最开始是建立以$\{P_i, P_j\}$确定下来的两点覆盖圆,从$P_1$开始逐个检查$P_k$($k < j$)在不在之前的最小覆盖圆内,不在说明$P_k$在点集$\{P_i, P_j, P_1, \dots, P_k\}$的最小覆盖圆边界上。一个圆至多由边界上的三个点确定,此时已经可以确定边界上的三个点,那么这个圆已经完全被确定下来了。也就是说,在求经过两点$\{P_i, P_j\}$的点集$\{P_i, P_j, P_1, \dots, P_{j-1}\}$的最小覆盖圆,只需要找有没有剩下一个可能存在的边界点,把$P_1$到$P_{j-1}$遍历一遍就能求出过点$P_i$的点集$\{P_i, P_1, \dots, P_j\}$的最小覆盖圆。
既然对于任意$j < i$,都能求出过点$P_i$的点集$\{P_i, P_1, \dots, P_j\}$的最小覆盖圆,那么$j$一直拓展到$i-1$,就能求得点集$\{P_1, P_2, \dots, P_i\}$的最小覆盖圆。把$i$一直拓展到整体点集的个数$n$,最后就能得到整体点集的最小覆盖圆。
现在你已经理解了这个算法的“增量”部分,“随机”部分又是什么呢?如果对算法进行分析,总是可以设计出一种最坏的输入,让算法每一步拓展点集的时候都需要重新构造新点集的最小覆盖圆,这样算法的时间复杂度不能到线性。为了实现在期望上能有线性的时间复杂度,我们要把输入随机打乱。所以在拿到点集时,我们需要对点集的顺序进行一次随机打乱。
伪代码
接下来将用三个流程的伪代码展示整个算法是怎么进行的。
Algorithm 1: 计算最小覆盖圆 (主流程)
─────────────────────────────────────────────────────────────────
Input:
一个非空点集 P = {P₁, ..., Pₙ}, 其中 n = |P|.
一个空的边界点集 B = ∅.
Output:
点集 P 的最小覆盖圆 C.
function CalculateMEC(P, B)
// 前置条件: B = ∅ 且 P ≠ ∅
1: 随机打乱点集 P 的顺序
2: if n = 1 then return 以 P₁ 为圆心, r=0 的圆
3: C ← 由 P₁ 和 P₂ 构成的最小覆盖圆
4: for k = 3 to n do
5: if 点 Pₖ 位于圆 C 外部 then
6: C ← CalculateMEC({P₁, ..., Pₖ₋₁}, {Pₖ})
7: end if
8: end for
9: return C
end function
Algorithm 2: 计算最小覆盖圆 (已知一个边界点)
─────────────────────────────────────────────────────────────────
Input:
一个非空点集 P' = {P'₁, ..., P'ₘ}, 其中 m = |P'|.
包含一个边界点的集合 B = {Q}.
Output:
覆盖 P' 且以 Q 为边界点的最小覆盖圆 C'.
function CalculateMEC(P', B)
// 前置条件: |B|=1 且 P' ≠ ∅
1: C' ← 由 Q 和 P'₁ 构成的最小覆盖圆
2: for j = 2 to m do
3: if 点 P'ⱼ 位于圆 C' 外部 then
4: C' ← CalculateMEC({P'₁, ..., P'ⱼ₋₁}, {Q, P'ⱼ})
5: end if
6: end for
7: return C'
end function
Algorithm 3: 计算最小覆盖圆 (已知两个边界点)
─────────────────────────────────────────────────────────────────
Input:
一个非空点集 P'' = {P''₁, ..., P''ₗ}, 其中 l = |P''|.
包含两个边界点的集合 B = {Q₁, Q₂}.
Output:
覆盖 P'' 且以 Q₁, Q₂ 为边界点的最小覆盖圆 C''.
function CalculateMEC(P'', B)
// 前置条件: |B|=2 且 P'' ≠ ∅
1: C'' ← 由 Q₁ 和 Q₂ 构成的最小覆盖圆
2: for i = 1 to l do
3: if 点 P''ᵢ 位于圆 C'' 外部 then
4: C'' ← 由 Q₁, Q₂, P''ᵢ 三点确定的圆
5: end if
6: end for
7: return C''
end function
理论推导
这一节将会对算法的正确性进行一个简单而严谨的证明,并对算法时间复杂度进行推导。
算法正确性
最小覆盖圆的唯一性
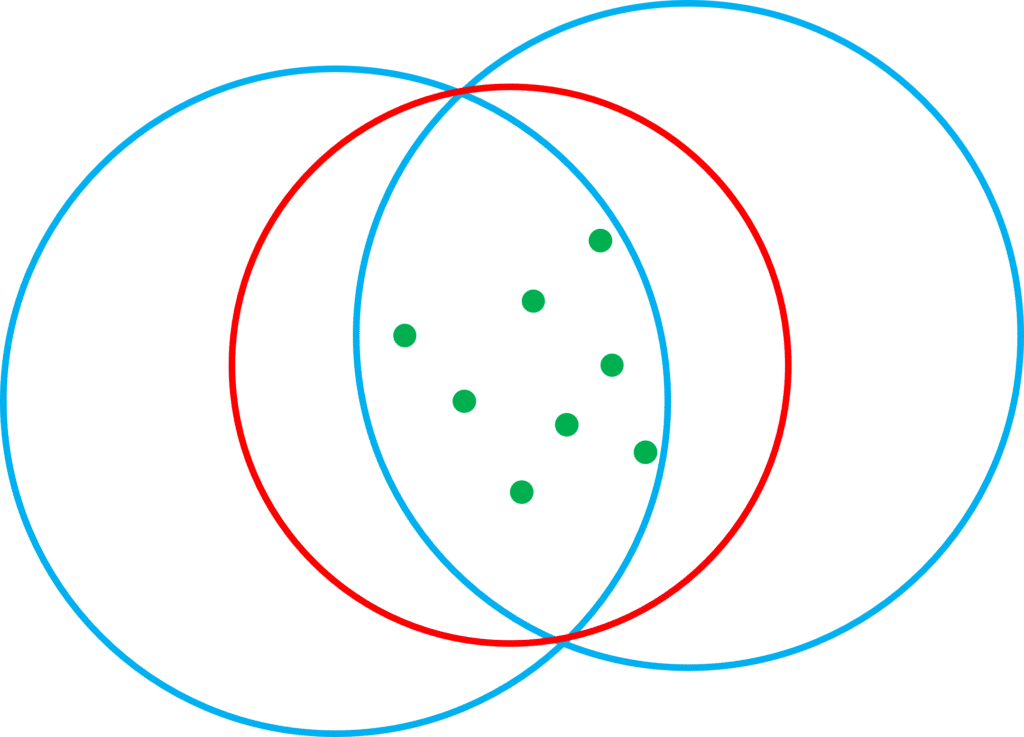
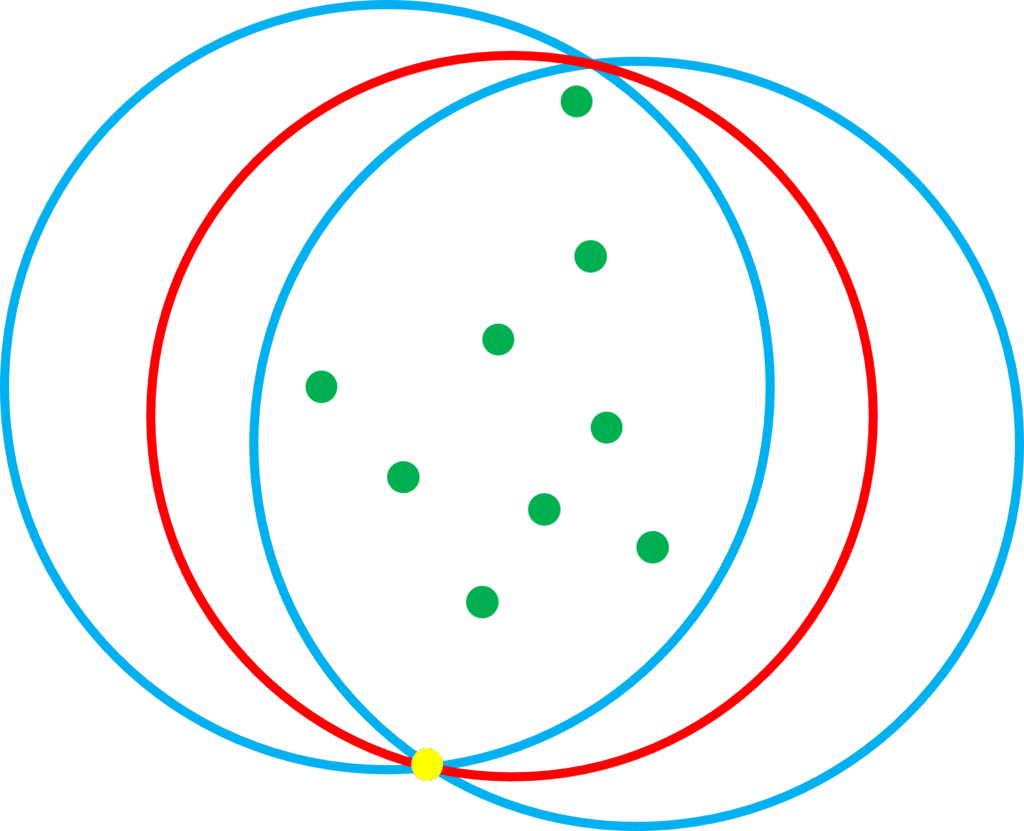
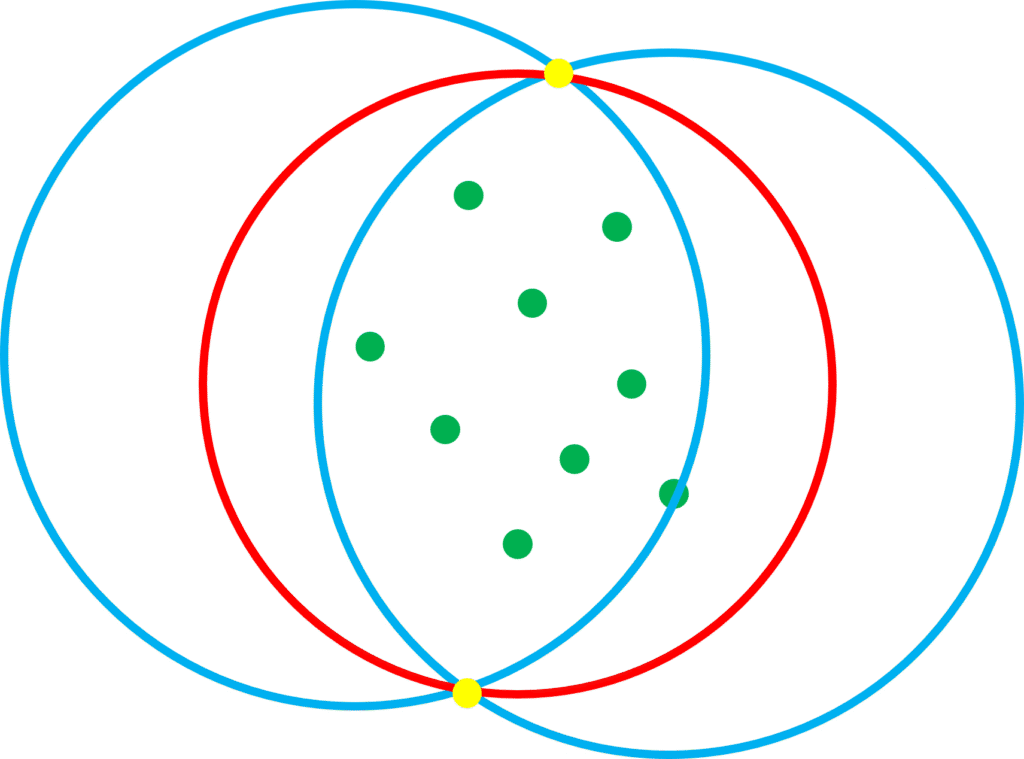
给定一个点集,它的最小覆盖圆是不是唯一的?半径一定是唯一的,那么圆心的位置是不是唯一的?答案是肯定的。如果一个点集具有两个相同半径的最小覆盖圆,我总能在两个圆公共部分构造出一个更小的圆,这就说明之前两个最小覆盖圆并不是最小的,发生矛盾,所以最小覆盖圆的圆心位置也是唯一的。可以看下图,三种情况分别是需要过0个点、1个点、2个点的最小覆盖圆情况,绿色的点为一般点,黄色的点为必须经过的点。如果存在两个半径相同的最小覆盖圆,即图中蓝色的圆,我总能以两个圆的公共弦为直径,构造出红色的新覆盖圆,红色圆是比蓝色圆更小的。
最小覆盖圆的充要条件
对于一个点数大于1的平面点集来说,一个圆是它的最小覆盖圆的充要条件是两个点在边界上且这两个点的线段是这个圆的直径,或者至少三个点在圆的边界上且此时边界上的点一定能找到三点,这三点构成一个锐角三角形或者直角三角形。我们现在要证明这个性质。
接下来说明必要性。如果一个点集的覆盖圆是最小覆盖圆,那么覆盖圆上面一定有两个点且这两个点的线段是覆盖圆的直径,或者存在三个以上的点且这些边界点中存在三个点构成的三角形是直角三角形或者锐角三角形。
我们首先要说明如果边界上不足两个点,那么一定不是最小覆盖圆。利用最小覆盖圆的唯一性可以轻松证明。如果一个圆边界上一个点都没有,那么我任意取一个方向,一定可以找到一个充分小的距离对覆盖圆进行平移,此时圆依然对点集形成覆盖,就有两个半径相同的覆盖圆了;如果一个圆边界上只有一个点,那么可以让圆以一个足够小的角度围绕边界点进行旋转,旋转之后依然对点集进行覆盖,这样也形成了两个半径相同的覆盖圆。由最小覆盖圆的唯一性,如果圆的边界上只有少于两个点,那么这个圆一定不是最小覆盖圆。也就是最小覆盖圆边界上一定至少有两个点。可以看下面图片的左边两张图,如果没有点或者只有一个点在边界上,我们可以得到一个半径相同的另一个覆盖圆,从而当前圆不是最小覆盖圆。
接下来我们要说明如果是最小覆盖圆边界上只有两个点,那么这两个点的线段一定是圆的直径。如果不是直径,我们可以以这条线段为弦,在这条弦的中垂线上让圆心向弦的方向移动一个充分小的距离,使得新的圆依然是点集的覆盖圆。如果这条弦不是直径,那么圆心移动后,直径会变短,覆盖圆也就变小了,这说明原来的圆不是最小覆盖圆。我们也就说明了最小覆盖圆边界上如果只有两个点,那么这两个点的线段一定是圆的直径。可以看下面图片第三张,如果圆只过两点并且这个两点的线段不是直径,那么我可以构造出半径更小的覆盖圆,说明原来的圆不是最小覆盖圆。
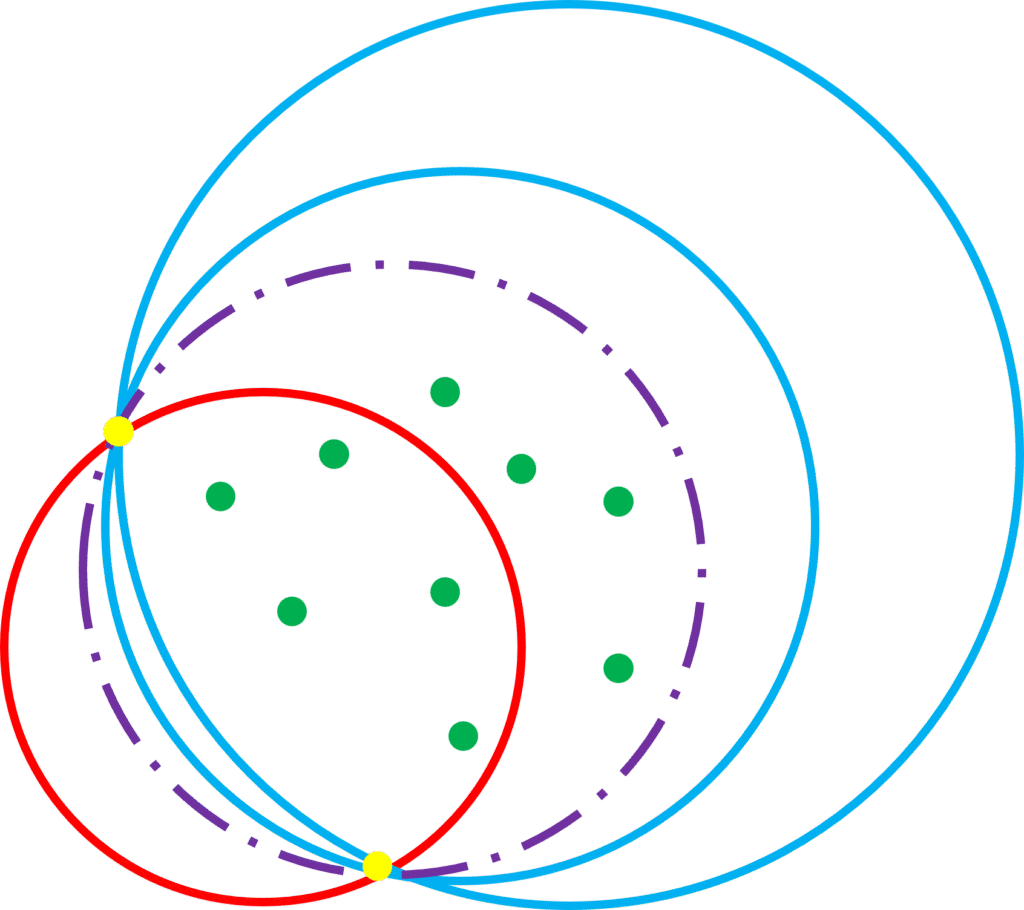
我们还需要说明如果最小覆盖圆上面有三个以上的点,那么一定能找到边界上的三个点,这三个点构成锐角三角性或者直角三角形。我们采取反证法,加入任意取边界上的三个点都是钝角三角形,那么这个覆盖圆不是最小覆盖圆。如果边界上的点任意取三点构成的三角形都是钝角三角形,说明存在一条直径可以让这些边界点都在直径的同一边。此时我可以让覆盖圆沿着直径垂直方向平移,平移一个充分小的距离后依然覆盖点集。两个半径相同的覆盖圆说明原来的覆盖圆不是最小覆盖圆。可以看下面图片最右边一张,展示了这种过程。



必要性已经证明完毕,接下来说明充分性。假入一个点集的覆盖圆满足边界上有两个点且这两个点的线段是覆盖圆的直径,或者边界上有三个以上的点且这些边界点存在三个点构成的三角形是直角三角形或者锐角三角形,那么这个覆盖圆是最小覆盖圆。
三个点构成直角三角形和两个点是直径其实是一种情况,我们看两个点形成覆盖圆直径的情况:所有覆盖圆一定会覆盖这两个点形成的线段,而只有在这条线段是直径的时候,这个圆才最小,所以此时一定是最小覆盖圆。再来看存在三个边界点构成锐角三角形的情况:此时我们只看这三个点,由在必要性里面已经证明了的最小覆盖圆的性质,这三个点的最小覆盖圆一定是两个点作直径或者三个点确定的圆,而显然任意一边做直径都无法覆盖另一个点,所以只能是这三个点确定的圆;对于整个点集来说,一个三个点的子点集的最小覆盖圆就是当前的覆盖圆了,当然不能找到一个更小的覆盖圆了,说明当前覆盖圆是点集的最小覆盖圆。到此充分性得证。
由此,充要性得证。
最小覆盖圆由边界点支撑
如果一个点集删去了一个不在最小覆盖圆边界上的点,新点集的最小覆盖圆不变。
这个性质其实很好证明,由前面的性质,我们已经知道一个点集的最小覆盖圆要不然由形成最小覆盖圆直径的两个点或者内接锐角三角形的三个点确定,那么删去一个边界上的点,自然没有删去这些起确定作用的点。删去一个不在边界上的点后,之前的最小覆盖圆还是新点集的覆盖圆,并且还满足最小覆盖圆的充分条件,那么这个覆盖圆就还是新点集的最小覆盖圆。由此得证。
增量策略的正确性
基于随机增量的最小圆覆盖算法核心在于这个“增量”,也就是当加入一个点进来时判断这个点在不在原来的最小覆盖圆,在就保持最小覆盖圆;不在就能得到当前点在当前点集的最小覆盖圆的边界上的信息,利用这个信息可以高效找到当前点集的最小覆盖圆。这样的增量策略为什么是正确的呢,这里给出说明。
如果新的点在原来的最小覆盖圆内,那么这个圆自然是新点集的最小覆盖圆,并且满足最小覆盖圆的充分条件,当然就是新点集的最小覆盖圆。如果新的点不在原来的最小覆盖圆内,我们需要它在新的最小覆盖圆边界上:首先,新的最小覆盖圆半径不会小于原来的最小覆盖圆(增加了一个点当然不会更小了),并且不会等于(如果这样原来的点集就会有两个半径相同的最小覆盖圆,这和唯一性矛盾),只能半径变大;那么对于这个新点集,删去新点,最小覆盖圆会变小(就是回到了原来的最小覆盖圆);如果新点不在新最小覆盖圆的边上,就只能在内部,有前一个性质,删去内部的点最小覆盖圆不变,与我们变小的论述是矛盾的,由此推出新点必定在新最小覆盖圆的边上。
我们这里只是论述了流程1里的增量策略是正确的,那么为什么流程2和流程3也是正确的呢?我们可以这样理解:对于点集$\{P_1, P_2, \dots, P_i\}$,我们已经知道$P_i$是这个点集边界上的点,它还需要找到另一个点形成直径或者另两个点形成锐角三角形从而找到当前点集的最小覆盖圆。我们假设确定当前点集的最小覆盖圆是两个形成直径的点确定的,那么$P_i$是直径上的一点,它还需要找到另外一点(如果$P_i$不是直径上端点,那么当前点集点集去掉$P_i$的最小覆盖圆就是这个直径确定的圆,它是会包含$P_i$的),而流程2一定能在遇到另一个直径上的点发现它在圆外,从而把它加入边界点集进入流程3,后面检查其他点都会在这条直径确定的圆都会覆盖,从而最终确定出这个最小覆盖圆。假设当前点集的最小覆盖圆是三个形成锐角三角形确定的,那么$P_i$是其中一点(和前面是直径端点一样的思路),假设另外两点是$P_k$和$P_j$($k < j < i$),那么流程2在遇到加入$P_j$时会发现它不在最小覆盖圆里面,则会把$P_i$和$P_j$加入边界点进入流程3,流程3在遇到加入$P_k$时在圆外面,则最终会构造出以$P_i$,$P_j$,$P_k$确定的最小覆盖圆,剩下的验证均能通过。由此,我们就能说明整个算法流程时正确的。
上一段的推导可谓道出了本文算法的本质:你也可以类似分两种情况,整体点集的最小覆盖圆是由某一条直径的两点或者内接锐角三角形的三点确定的,那么按照算法流程,一定能找出三个点确定的最小覆盖圆。
由此,算法正确性得以证明。
时间复杂度
接下来我们将推导本文算法是在期望上具有线性时间复杂度的。我们将采用 “向后分析” 的策略,从最内层的递归(已知 2 个边界点)开始,逐层向外分析。
这是递归的终点。该流程是一个确定性的线性扫描,对 $n$ 个非边界点进行迭代,每次迭代执行 $O(1)$ 操作,因此其时间复杂度为:
$$T_2(n)=\mathcal{O}(n).$$在处理第 $i$ 个点时,它会以一定概率调用 $T_2(i-1)$。这个概率取决于第 $i$ 个点是否成为新 MEC 的边界点。由于 MEC 最多由另外 2 个点决定,且点集是随机的,所以该概率为 $2/i$。
因此,第 $i$ 步的期望耗时 $E_i$ 的计算式为:
$$E_i=\mathcal{O}(1)+\frac{2}{i}\,T_2(i-1) =\mathcal{O}(1)+\frac{2}{i}\cdot \mathcal{O}(i-1) =\mathcal{O}(1).$$对所有 $n$ 步求和,可得总期望时间:
$$\mathbb{E}[T_1(n)]=\sum_{i=1}^{n}\mathcal{O}(1)=\mathcal{O}(n).$$同理,在处理第 $k$ 个点时,它会以一定概率调用 $T_1(k-1)$。无约束的 MEC 最多由 3 个点决定,因此该概率为 $3/k$。
第 $k$ 步的期望耗时 $E_k$ 的计算式为:
$$E_k=\mathcal{O}(1)+\frac{3}{k}\,\mathbb{E}[T_1(k-1)] =\mathcal{O}(1)+\frac{3}{k}\cdot \mathcal{O}(k-1) =\mathcal{O}(1).$$对所有 $n$ 步求和,可得总期望时间:
$$\mathbb{E}[T_0(n)]=\sum_{k=1}^{n}\mathcal{O}(1)=\mathcal{O}(n).$$结论:通过以上推导,我们得出该算法的期望时间复杂度为 $\mathcal{O}(n)$,即线性时间。
代码实现
递归执行
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include <algorithm>
#include <random>
// 用于浮点数比较的精度阈值
const double EPS = 1e-12;
// --- 数据结构定义 ---
// Point 结构体,用于表示二维平面上的点
struct Point {
double x, y;
};
// Circle 结构体,用于表示圆(圆心和半径)
struct Circle {
Point center;
double radius;
};
// --- 必备的几何计算辅助函数 ---
/**
* @brief 计算两点之间的距离的平方。
* @param p1 第一个点
* @param p2 第二个点
* @return 两点距离的平方。使用平方可以避免开方运算,提高精度和效率。
*/
double dist_sq(const Point& p1, const Point& p2) {
return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);
}
/**
* @brief 构造一个以两点为直径的圆。
* @param p1, p2 构成直径的两个点。
* @return 覆盖这两点的最小圆。
*/
Circle get_circle_2pts(const Point& p1, const Point& p2) {
Point center = {(p1.x + p2.x) / 2.0, (p1.y + p2.y) / 2.0};
double radius = std::sqrt(dist_sq(p1, p2)) / 2.0;
return {center, radius};
}
/**
* @brief 构造一个由三点确定的圆(外接圆)。
* @param p1, p2, p3 三个点。
* @return 覆盖这三点的最小圆。
*/
Circle get_circle_3pts(const Point& p1, const Point& p2, const Point& p3) {
double a1 = 2 * (p2.x - p1.x), b1 = 2 * (p2.y - p1.y);
double c1 = p2.x * p2.x + p2.y * p2.y - p1.x * p1.x - p1.y * p1.y;
double a2 = 2 * (p3.x - p2.x), b2 = 2 * (p3.y - p2.y);
double c2 = p3.x * p3.x + p3.y * p3.y - p2.x * p2.x - p2.y * p2.y;
double det = a1 * b2 - a2 * b1;
// 如果三点共线,则以距离最远的两点构成直径圆
if (std::abs(det) < EPS) {
double d12 = dist_sq(p1, p2), d13 = dist_sq(p1, p3), d23 = dist_sq(p2, p3);
if (d12 >= d13 && d12 >= d23) return get_circle_2pts(p1, p2);
if (d13 >= d12 && d13 >= d23) return get_circle_2pts(p1, p3);
return get_circle_2pts(p2, p3);
}
double cx = (c1 * b2 - c2 * b1) / det;
double cy = (a1 * c2 - a2 * c1) / det;
Point center = {cx, cy};
double radius = std::sqrt(dist_sq(p1, center));
return {center, radius};
}
// --- 算法核心实现(递归流程) ---
// 为了让三个流程能相互调用,需要提前声明
Circle mec_with_2_points(const std::vector<Point>& P_prefix, const Point& q1, const Point& q2);
Circle mec_with_1_point(const std::vector<Point>& P_prefix, const Point& q);
/**
* @brief 流程3: 已知两个边界点,求最小覆盖圆。
* @param P_prefix 待覆盖的点集(实际上是原始点集的前缀)。
* @param q1, q2 两个已知的边界点。
* @return 覆盖 P_prefix 和 {q1, q2} 且 q1, q2 在边界上的最小圆。
*/
Circle mec_with_2_points(const std::vector<Point>& P_prefix, const Point& q1, const Point& q2) {
// 初始圆由两个边界点构成
Circle mec = get_circle_2pts(q1, q2);
// 遍历所有已处理的点
for (const auto& p : P_prefix) {
// 如果点 p 在当前圆外,则新圆由 q1, q2, p 三点确定
if (dist_sq(p, mec.center) > mec.radius * mec.radius + EPS) {
mec = get_circle_3pts(q1, q2, p);
}
}
return mec;
}
/**
* @brief 流程2: 已知一个边界点,求最小覆盖圆。
* @param P_prefix 待覆盖的点集。
* @param q 一个已知的边界点。
* @return 覆盖 P_prefix 和 {q} 且 q 在边界上的最小圆。
*/
Circle mec_with_1_point(const std::vector<Point>& P_prefix, const Point& q) {
// 初始圆由边界点q和第一个点p[0]构成
Circle mec = get_circle_2pts(P_prefix[0], q);
// 遍历从第二个点到当前最后一个点
for (size_t i = 1; i < P_prefix.size(); ++i) {
// 如果点 P_prefix[i] 在当前圆外,则调用流程3
// 新的边界点是 q 和 P_prefix[i]
if (dist_sq(P_prefix[i], mec.center) > mec.radius * mec.radius + EPS) {
std::vector<Point> subset(P_prefix.begin(), P_prefix.begin() + i);
mec = mec_with_2_points(subset, q, P_prefix[i]);
}
}
return mec;
}
/**
* @brief 流程1: 主接口和主流程,计算点集的最小覆盖圆。
* @param points 输入的点集。
* @return 覆盖所有点的最小圆。
*/
Circle minimum_enclosing_circle(std::vector<Point>& points) {
// 关键步骤:随机打乱点集
std::random_device rd;
std::mt19937 g(rd());
std::shuffle(points.begin(), points.end(), g);
if (points.empty()) {
return {{0, 0}, 0};
}
if (points.size() == 1) {
return {points[0], 0};
}
// 初始圆由前两个点构成
Circle mec = get_circle_2pts(points[0], points[1]);
// 从第三个点开始增量计算
for (size_t i = 2; i < points.size(); ++i) {
// 如果点 points[i] 在当前圆外,则调用流程2
// 新的边界点是 points[i]
if (dist_sq(points[i], mec.center) > mec.radius * mec.radius + EPS) {
std::vector<Point> subset(points.begin(), points.begin() + i);
mec = mec_with_1_point(subset, points[i]);
}
}
return mec;
}
// --- Main 函数:处理输入输出 ---
int main() {
// 提高cin/cout效率
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
int n;
std::cin >> n;
std::vector<Point> points(n);
for (int i = 0; i < n; ++i) {
std::cin >> points[i].x >> points[i].y;
}
// 调用接口函数计算最小覆盖圆
Circle result_circle = minimum_enclosing_circle(points);
// 设置输出精度并打印结果
std::cout << std::fixed << std::setprecision(10) << result_circle.radius << std::endl;
std::cout << std::fixed << std::setprecision(10) << result_circle.center.x << " " << result_circle.center.y << std::endl;
return 0;
}
递推执行
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include <algorithm>
#include <random>
// 用于浮点数比较的精度阈值
const double EPS = 1e-12;
// --- 数据结构定义 ---
// Point 结构体,表示二维平面上的点
struct Point {
double x, y;
};
// Circle 结构体,存储圆心和半径的平方
struct Circle {
Point center;
double radius_sq; // 存储半径的平方以避免频繁开方
};
// --- 必备的几何计算辅助函数 ---
/**
* @brief 计算两点之间的距离的平方。
* @param p1 第一个点
* @param p2 第二个点
* @return 两点距离的平方。
*/
inline double dist_sq(const Point& p1, const Point& p2) {
return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);
}
/**
* @brief 构造一个以两点为直径的圆。
* @param p1, p2 构成直径的两个点。
* @return 覆盖这两点的最小圆。
*/
Circle get_circle_2pts(const Point& p1, const Point& p2) {
Point center = {(p1.x + p2.x) / 2.0, (p1.y + p2.y) / 2.0};
double r_sq = dist_sq(p1, center);
return {center, r_sq};
}
/**
* @brief 构造一个由三点确定的圆(外接圆)。
* @param p1, p2, p3 三个点。
* @return 覆盖这三点的最小圆。
*/
Circle get_circle_3pts(const Point& p1, const Point& p2, const Point& p3) {
double a1 = 2 * (p2.x - p1.x), b1 = 2 * (p2.y - p1.y);
double c1 = p2.x * p2.x + p2.y * p2.y - p1.x * p1.x - p1.y * p1.y;
double a2 = 2 * (p3.x - p2.x), b2 = 2 * (p3.y - p2.y);
double c2 = p3.x * p3.x + p3.y * p3.y - p2.x * p2.x - p2.y * p2.y;
double det = a1 * b2 - a2 * b1;
// 如果三点共线,退化为两点定圆问题
if (std::abs(det) < EPS) {
double d12 = dist_sq(p1, p2), d13 = dist_sq(p1, p3), d23 = dist_sq(p2, p3);
if (d12 >= d13 && d12 >= d23) return get_circle_2pts(p1, p2);
if (d13 >= d12 && d13 >= d23) return get_circle_2pts(p1, p3);
return get_circle_2pts(p2, p3);
}
double cx = (c1 * b2 - c2 * b1) / det;
double cy = (a1 * c2 - a2 * c1) / det;
Point center = {cx, cy};
double r_sq = dist_sq(p1, center);
return {center, r_sq};
}
/**
* @brief 最小覆盖圆算法的高效迭代实现。
* @param points 输入的点集。
* @return 覆盖所有点的最小圆。
*/
Circle minimum_enclosing_circle_iterative(std::vector<Point>& points) {
// 关键步骤:随机打乱点集
std::random_device rd;
// --- 修正点在这里 ---
std::mt19937 g(rd()); // mt19_37 -> mt19937
// --- 修正结束 ---
std::shuffle(points.begin(), points.end(), g);
size_t n = points.size();
if (n == 0) return {{0, 0}, 0};
if (n == 1) return {points[0], 0};
// 初始圆由前两个点构成
Circle mec = get_circle_2pts(points[0], points[1]);
// --- 主流程:三层嵌套循环,对应0, 1, 2个边界点约束 ---
// i循环: 确定0个边界点 -> 1个边界点
for (size_t i = 2; i < n; ++i) {
// 如果点i在当前圆外,则它必然是新圆的边界点
if (dist_sq(points[i], mec.center) > mec.radius_sq + EPS) {
// 流程2的开始: 已知 points[i] 是边界点
// 用 points[i] 和 points[0] 构造初始圆
mec = get_circle_2pts(points[i], points[0]);
// j循环: 确定1个边界点 -> 2个边界点
for (size_t j = 1; j < i; ++j) {
// 如果点j在当前圆外,则它和points[i]必然是新圆的边界点
if (dist_sq(points[j], mec.center) > mec.radius_sq + EPS) {
// 流程3的开始: 已知 points[i] 和 points[j] 是边界点
// 用 points[i] 和 points[j] 构造初始圆
mec = get_circle_2pts(points[i], points[j]);
// k循环: 寻找第三个边界点
for (size_t k = 0; k < j; ++k) {
// 如果点k在当前圆外,则新圆由 i, j, k 三点确定
if (dist_sq(points[k], mec.center) > mec.radius_sq + EPS) {
mec = get_circle_3pts(points[i], points[j], points[k]);
}
}
}
}
}
}
return mec;
}
// --- Main 函数:处理输入输出 ---
int main() {
// 提高cin/cout效率
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
int n;
std::cin >> n;
std::vector<Point> points(n);
for (int i = 0; i < n; ++i) {
std::cin >> points[i].x >> points[i].y;
}
// 调用接口函数计算最小覆盖圆
Circle result_circle = minimum_enclosing_circle_iterative(points);
// 设置输出精度并打印结果 (注意最后开方)
std::cout << std::fixed << std::setprecision(10) << std::sqrt(result_circle.radius_sq) << std::endl;
std::cout << std::fixed << std::setprecision(10) << result_circle.center.x << " " << result_circle.center.y << std::endl;
return 0;
}